无线加速度传感器 - 2
- 适配 MPU6050
用 MPU 6050 和 ESP8266-01S 制作一个无线加速度传感器
MPU6050 已经在上一章完成驱动,但可以看到,它的静态读数为(-0.11,-0.25,8.96),并不是 9.8 的重力加速度,所以现在,我需要对这个数据进行处理,主要是零漂和抖动。
零漂
零漂就是在静止状态下的漂移,校准零漂类似于「调零」。
方法验证
我想到的解决办法是解方程组:
作为读取的数据, 是三轴的偏移量。
实际上解这个三元二次方程是很难的,我先带了三个
得到方程组:
但是我把这个输入 Microsoft MathSolver 它说表达式有问题,其实后来我知道这是个函数不能解出精确值,只能逼近估算。所以我找了个三维函数绘制器
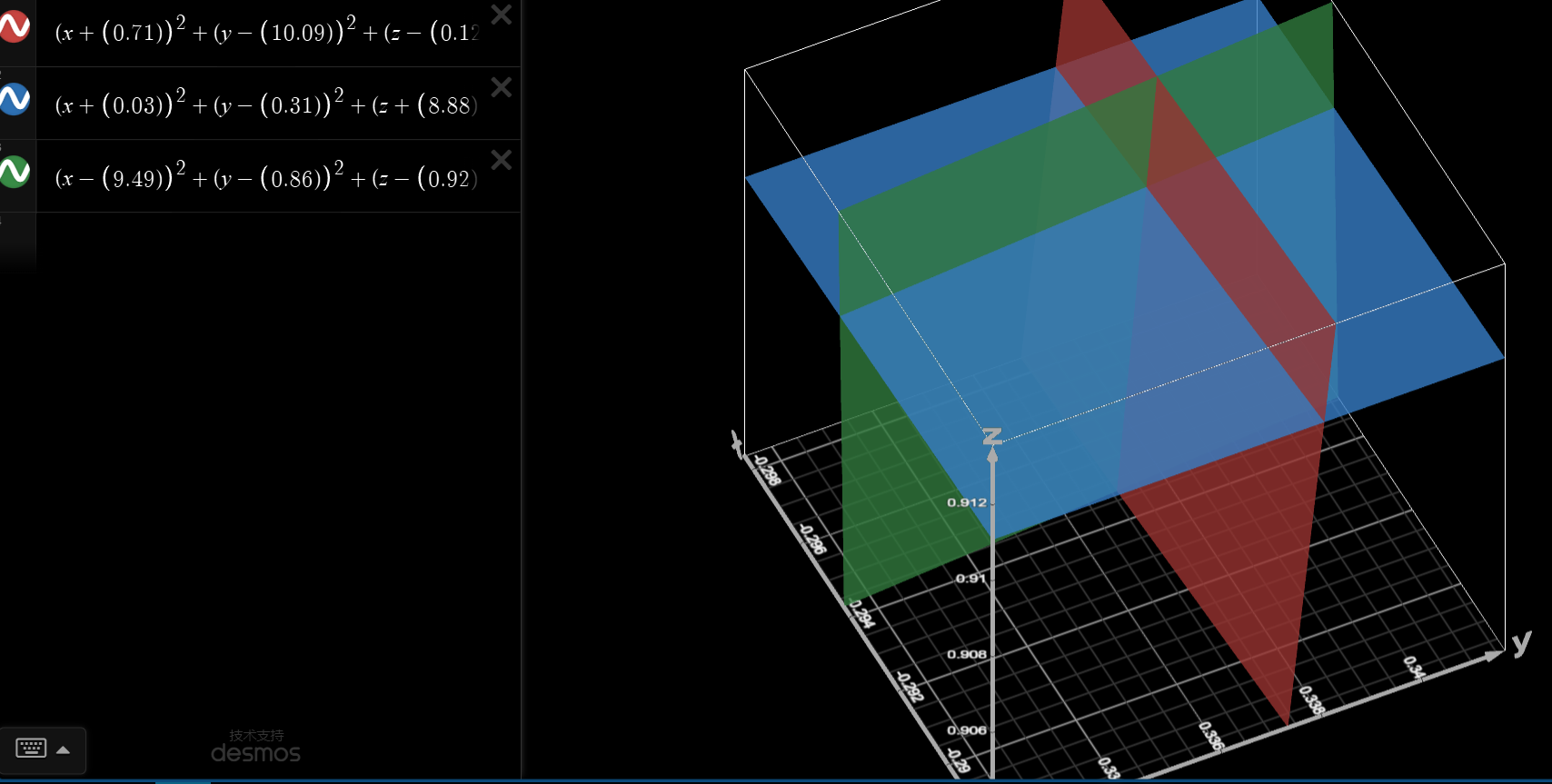 放大放大再放大,读出交点为 即为漂移量 (Offset)。
回带数据:
放大放大再放大,读出交点为 即为漂移量 (Offset)。
回带数据:
(-3.51,-5.67,6.38)==>(-3.81,-5.33,7.29)==>9.80148
(2.01,5.07,7.12)==>(1.71,5.41,8.03)==>9.8322
(-0.16,8.58,3.33)==>(-0.46,8.92,4.24)==>9.887
接近重力加速度 9.8 验证方法可行。
方程解算
牛顿迭代
这个三元一次方程求解时我有想到 GPS 定位也是类似的解算方法,于是在网上搜索了一番,发现可以用「牛顿迭代」,但是太难,没看懂,弃。
枚举法
退而求其次使用枚举法,Python代码:
# (-0.3,0.34,0.91)
#定义原数据
d1=[0.03,-0.31,8.88]
d2=[-9.49,-0.86,-0.92]
d3=[0.71,-10.09,-0.12]
#计算精确度
resut = [[[0 for _ in range(20)] for _ in range(20)] for _ in range(20)]
for i in range(-10,10):
for j in range(-10,10):
for k in range(-10,10):
resut[i+10][j+10][k+10] = abs((0.1*i +d1[0])**2+(0.1*j+d1[1])**2+(0.1*k+d1[2])-9.8**2)+abs((0.1*i +d2[0])**2+(0.1*j+d2[1])**2+(0.1*k+d2[2])-9.8**2)+abs((0.1*i +d3[0])**2+(0.1*j+d3[1])**2+(0.1*k+d3[2])-9.8**2)
#找到最接近的值
minn=100000.0000
for i in range(-10,10):
for j in range(-10,10):
for k in range(-10,10):
if(resut[i+10][j+10][k+10]<minn):
minn=resut[i+10][j+10][k+10]
x=i
y=j
z=k
print(minn,x,y,z)
运行结果
86.9415 -3 3 8
(-0.3,0.3,0.8)接近了,还不够,但现在运行的精度0.1已经运行了 次带有九个乘方的代码,还要给 个 Float 比大小。使用至少 SRAM,再提高精度会使内存占用立方上涨,所以弃用此方法。
「八分法」
效仿二分法,将给定一个立方体,示例为 作为逼近区间
27点法
将区间切分为8个小矩形,取小矩形的共27个顶点:
任然带之前的数据,得到(整数化后,方便观察):
再将每个小矩形对应的八个数相加,作为它的误差总和,然后选取最小误差总和的数作为下一次八分区间,Python程序:
# (−0.3,0.34,0.91)
#定义原数据
# (−0.3,0.34,0.91)
#定义原数据
d1=[0.03,-0.31,8.88]
d2=[-9.49,-0.86,-0.92]
d3=[0.71,-10.09,-0.12]
c=0.0001#精确度
ba=[[-2,-2,-2],[2,2,2]]#给定区间(小到大)
a=ba
result = [[[0 for _ in range(3)] for _ in range(3)] for _ in range(3)]
block = [[[0 for _ in range(2)] for _ in range(2)] for _ in range(2)]
while (a[1][0]-a[0][0] >=c ):
dd=0
for i in [a[0][0],(a[0][0]+a[1][0])/2,a[1][0]]:
for j in [a[0][1],(a[0][1]+a[1][1])/2,a[1][1]]:
for k in [a[0][2],(a[0][2]+a[1][2])/2,a[1][2]]:
result[int(dd/9)][int(dd/3)%3][dd%3] = abs((i+d1[0])**2+(j+d1[1])**2+(k+d1[2])**2-96.04)**(1/2)+abs((i+d2[0])**2+(j+d2[1])**2+(k+d2[2])**2-96.04)**(1/2)+abs((i+d3[0])**2+(j+d3[1])**2+(k+d3[2])**2-96.04)**(1/2)
#一次加权误差值
dd=dd+1
#计算小区间的误差
for i in range(2):
for j in range(2):
for k in range(2):
block[i][j][k] = result[i][j][k]+result[i][j][k+1]+result[i][j+1][k]+result[i][j+1][k+1]+result[i+1][j][k]+result[i+1][j][k+1]+result[i+1][j+1][k]+result[i+1][j+1][k+1]
#找到最小的小区间
minn=100000.0
x,y,z=0,0,0
for i in range(2):
for j in range(2):
for k in range(2):
if(block[i][j][k]<minn):
minn=block[i][j][k]
x=i
y=j
z=k
#定义下一个八分区间
a=[[a[0][0] if x==0 else (a[0][0]+a[1][0])/2,a[0][1] if y==0 else (a[0][1]+a[1][1])/2,a[0][2] if z==0 else (a[0][2]+a[1][2])/2],[(a[0][0]+a[1][0])/2 if x==0 else a[1][0],(a[0][1]+a[1][1])/2 if y==0 else a[1][1],(a[0][2]+a[1][2])/2 if z==0 else a[1][2]]]
#用中间数赋值结果
ox,oy,oz = (a[1][0]+a[0][0])/2,(a[1][1]+a[0][1])/2,(a[1][2]+a[0][2])/2
print(ox,oy,oz)
结果(-0.2957,0.3312,0.9163)显然逼近正确,
再带
三个非特殊姿态,再来进行解算,得(-0.21,0.41,0.91),还算可以。
可以作为一种备选方案,但把初始区间改大之后到 就会出现(0.000152587890625,0.316497802734375,-3.0517578125e-05),在八分时到了其他地方。
8点法
把区间分为8个小矩形,取矩形中点算值,原理类似27点法,而且测试精度更高……但我先想到27点法,没想到多带点反倒会干扰对错误数值的惩罚,8点法Python程序:
# (−0.3,0.34,0.91)
#定义原数据
# d1=[0.70,-4.33,8.05]
# d2=[-8.71,-1.24,-4.89]
# d3=[1.24,-9.20,-5.13]
# d1=[0.64, -0.30, 8.94]
# d2=[-9.33,-0.84,0.78]
# d3=[0.23,-8.94,3.71]
d1=[0.03,-0.31,8.88]
d2=[-9.49,-0.86,-0.92]
d3=[0.71,-10.09,-0.12]
c=0.0001#精确度
ba=[[-3,-3,-3],[3,3,3]]#给定区间(小到大)
a=ba
result = [[[0 for _ in range(2)] for _ in range(2)] for _ in range(2)]
while (a[1][0]-a[0][0] >=c ):
dd=0
ax,ay,az=a[1][0]-a[0][0],a[1][1]-a[0][1],a[1][2]-a[0][2],
for i in [a[0][0]+ax/4,a[0][0]+ax/4*3]:
for j in [a[0][1]+ay/4,a[0][1]+ay/4*3]:
for k in [a[0][2]+az/4,a[0][2]+az/4*3]:
result[int(dd/4)][int(dd/2)%2][dd%2] = abs((i+d1[0])**2+(j+d1[1])**2+(k+d1[2])**2-96.04)**(1/2)+abs((i+d2[0])**2+(j+d2[1])**2+(k+d2[2])**2-96.04)**(1/2)+abs((i+d3[0])**2+(j+d3[1])**2+(k+d3[2])**2-96.04)**(1/2)
#一次加权误差值
dd=dd+1
#找到最小的小区间
minn=100000.0
x,y,z=0,0,0
for i in range(2):
for j in range(2):
for k in range(2):
if(result[i][j][k]<minn):
minn=result[i][j][k]
x=i
y=j
z=k
#定义下一个八分区间
a=[[a[0][0] if x==0 else (a[0][0]+a[1][0])/2,a[0][1] if y==0 else (a[0][1]+a[1][1])/2,a[0][2] if z==0 else (a[0][2]+a[1][2])/2],[(a[0][0]+a[1][0])/2 if x==0 else a[1][0],(a[0][1]+a[1][1])/2 if y==0 else a[1][1],(a[0][2]+a[1][2])/2 if z==0 else a[1][2]]]
#用中间数赋值结果
ox,oy,oz = (a[1][0]+a[0][0])/2,(a[1][1]+a[0][1])/2,(a[1][2]+a[0][2])/2
print(ox,oy,oz)
至此,方程的解算算是完成了,现在需要把 Python 程序打包成 C语言 供 Arduino IDE 里使用。
找AI帮了下忙 废物AI,花了我几十分钟改正它的程序,不如自己写:
#include <math.h>
// 定义vector3结构
typedef struct {
float x;
float y;
float z;
} vector3;
float abss(float x){return (x<0)?(-x):x;}
float result[3][3][3]={0};
// 使用八分法求解偏移量的函数
vector3 offset_solve(vector3 d1, vector3 d2, vector3 d3, float c, vector3 s, vector3 e) {
while (e.x-s.x >=c)
{
float ax=e.x-s.x;float ay=e.y-s.y;float az=e.z-s.z;
float ix,iy,iz;
for (int i=0;i<2;i++){
for(int j=0;j<2;j++){
for(int k=0;k<2;k++){
if(i==0)ix=s.x+ax/4;else ix=s.x+ax/4*3;
if(j==0)iy=s.y+ay/4;else iy=s.y+ay/4*3;
if(k==0)iz=s.z+az/4;else iz=s.z+az/4*3;
float e1=sqrt(abss((ix+d1.x)*(ix+d1.x)+(iy+d1.y)*(iy+d1.y)+(iz+d1.z)*(iz+d1.z)-96.04));
float e2=sqrt(abss((ix+d2.x)*(ix+d2.x)+(iy+d2.y)*(iy+d2.y)+(iz+d2.z)*(iz+d2.z)-96.04));
float e3=sqrt(abss((ix+d3.x)*(ix+d3.x)+(iy+d3.y)*(iy+d3.y)+(iz+d3.z)*(iz+d3.z)-96.04));
result[i][j][k]=e1+e2+e3;
}}}
float minn=1000000.0;
int x,y,z;
for (int i=0;i<2;i++){
for(int j=0;j<2;j++){
for(int k=0;k<2;k++){
if(result[i][j][k]<minn){
minn=result[i][j][k];
x=i;y=j;z=k;
}
}}}
s.x=(x==0)?s.x:((s.x+e.x)/2);
s.y=(y==0)?s.y:((s.y+e.y)/2);
s.z=(z==0)?s.z:((s.z+e.z)/2);
e.x=(x==0)?((s.x+e.x)/2):e.x;
e.y=(y==0)?((s.y+e.y)/2):e.y;
e.z=(z==0)?((s.z+e.z)/2):e.z;
}
vector3 out = {(s.x+e.x)/2,(s.y+e.y)/2,(s.z+e.z)/2};
return out;
}
void setup(){
Serial.begin(115200);
}
void loop(){
vector3 d1={0.64, -0.30, 8.94};
vector3 d2={-9.33,-0.84,0.78};
vector3 d3={0.23,-8.94,3.71};
float c = 0.001;
vector3 s = {-1,-1,-1};
vector3 e = {1,1,1};
vector3 out = offset_solve(d1, d2, d3, c, s, e);
Serial.print(out.x);
Serial.print(",");
Serial.print(out.y);
Serial.print(",");
Serial.println(out.z);
delay(500);
}
成功打印出正确偏移量00:35:39.090 -> -0.31,0.29,0.90 ,零漂也算是不太完美的解决了。
